并查集初体验

背景

问题一 一共有 n 个数，编号是 1∼n，最开始每个数各自在一个集合中。

现在要进行 m 个操作，操作共有两种：

M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；

输入格式

第一行输入整数 n 和 m。

接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 a 和 b 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1≤n,m≤1051≤n,m≤105

输入样例：

4 5 M 1 2 M 3 4 Q 1 2 Q 1 3 Q 3 4

输出样例：

Yes No Yes

问题二 给定一个包含 n 个点（编号为 1∼n）的无向图，初始时图中没有边。

现在要进行 m 个操作，操作共有三种：

C a b，在点 a 和点 b 之间连一条边，a 和 b 可能相等； Q1 a b，询问点 a 和点 b 是否在同一个连通块中，a 和 b 可能相等； Q2 a，询问点 a 所在连通块中点的数量； 输入格式 第一行输入整数 n 和 m。

接下来 m 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

输出格式 对于每个询问指令 Q1 a b，如果 a 和 b 在同一个连通块中，则输出 Yes，否则输出 No。

对于每个询问指令 Q2 a，输出一个整数表示点 a 所在连通块中点的数量

每个结果占一行。

数据范围

1≤n,m≤1051≤n,m≤105

输入样例：

5 5 C 1 2 Q1 1 2 Q2 1 C 2 5 Q2 5

输出样例：

Yes 2 3

问题三 动物王国中有三类动物 A,B,C，这三类动物的食物链构成了有趣的环形。

A 吃 B，B 吃 C，C 吃 A。

现有 N 个动物，以 1∼N 编号。

每个动物都是 A,B,C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 N 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 X 和 Y 是同类。

第二种说法是 2 X Y，表示 X 吃 Y。

此人对 N 个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真的，有的是假的。

当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；
当前的话中 X 或 Y 比 N 大，就是假话；
当前的话表示 X 吃 X，就是假话。你的任务是根据给定的 N 和 K 句话，输出假话的总数。

输入格式 第一行是两个整数 N 和 K，以一个空格分隔。

以下 K 行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中 DD 表示说法的种类。

若 D=1，则表示 X 和 Y 是同类。

若 D=2，则表示 X 吃 Y。

输出格式 只有一个整数，表示假话的数目。

数据范围

1≤N≤50000 0≤K≤100000

输入样例：

100 7 1 101 1 2 1 2 2 2 3 2 3 3 1 1 3 2 3 1 1 5 5

输出样例：

3

算法核心思路

通过递归找到祖先节点压缩路径拓展处理压缩路径时父节点的状态（尤其是修改状态和祖先归并的先后顺序）如果状态可以分类的话，可以再尝试用周期记录状态 核心代码

int find (int x){
    if(p[x]!=x)p[x]=find(p[x]);
    return p[x];
    //p[x]为x的父节点，find(x)为x的祖先节点
}

不断递归压缩路径，最后达到任意子节点的父节点都是祖先节点

题解

问题一 源码

#include <iostream>

using namespace std;

const int N=1000010;

int p[N];

int find(int x){
    if(p[x]!=x)p[x]=find(p[x]);
    return p[x];
}

int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)p[i]=i;
    while(m--){
        char ch[2];
        int a,b;
        cin>>ch>>a>>b;
        if(ch[0]=='M'){
        p[find(a)]=find(b);
        }
        else if(ch[0]=='Q'){
            if(find(a)==find(b))cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }

    }
    return 0;
}

没什么好说的，只是单纯的套用了并查集的模板

问题二 源码

#include <iostream>

using namespace std;

const int N=100010;
int p[N];
int s[N];
int find (int x){
    if(p[x]!=x)p[x]=find(p[x]);
    return p[x];
}

int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
    p[i]=i;
    s[i]=1;
    }
    while(m--){
        string ch;
        int a,b;
        cin>>ch;
        if(ch=="C"){
            cin>>a>>b;
            if(find(a)==find(b))continue;
            s[find(b)]+=s[find(a)];
            p[find(a)]=find(b);

        }else if(ch=="Q1"){
            cin>>a>>b;
            if(find(a)==find(b))cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }else if(ch=="Q2"){
            cin>>a;
           cout<<s[find(a)]<<endl;
        }

    }
    return 0;
}

解题过程和反思 问题二在问题一的基础上添加了查找同类个数的要求一开始我直接暴力枚举 ~~不出意外~~超时了后来想了想可能会再开一个数组去记录每次合并后的个数状态自己写的时候出现了问题，但是几乎题解代码一模一样细看后发现了重点

if(ch=="C"){
            cin>>a>>b;
            if(find(a)==find(b))continue;
            s[find(b)]+=s[find(a)];
            p[find(a)]=find(b);
            //p[find(a)]=find(b);
            //s[find(b)]+=s[find(a)];
        }

注释掉的是我写的顺序确实出现了问题，如果先合并祖先，会导致我后面find(b)=find(a) 从而影响s[find(b)]+=s[find(a)]的结果（要想好状态转换和合并的顺序）（为下一题埋下伏笔）

问题三 （编码难度跨度挺大的，不过思路的理解还好）源码

#include <iostream>

using namespace std;

const int M=50010;

int p[M],d[M];

int find(int x){
    if(p[x]!=x){
    int tmp=find(p[x]);
    d[x]+=d[p[x]];
    p[x]=tmp;
    }return p[x];
}

int main(){
    int N,K; 
    int res=0;
    cin>>N>>K;
    for(int i=1;i<=N;i++)p[i]=i;
    while(K--){
        int a,b,t;

        cin>>t>>a>>b;

        if(a>N||b>N)res++;
        else {
        int pa=find(a);
        int pb=find(b);
        if(t==1){
            if(pa==pb&&(d[a]-d[b])%3)res++;
            else if(pa!=pb){
                p[pa]=pb;
                d[pa]=d[b]-d[a];
            }
        }else if(t==2){
            if(pa==pb&&(d[a]-d[b]-1)%3)res++;
            else if(pa!=pb){
                p[pa]=pb;
                d[pa]=d[b]+1-d[a];
            }
        }
        }
    }
    cout<<res<<endl;
    return 0;
}

解题过程和反思 对于我这种算法菜鸡来说一开始上手还是挺难的，最多做到合并同类对于处理谁吃谁或者说分类，没有任何思路直接看了题解，令人拍案叫绝同样多开了一个数组用来记录到到根节点的距离

距离余数为1则说明该类物质吃根节点
距离余数为2则说明根节点吃该类物质，同时该类物质吃距离余数为1的物质
距离余数为0则说明该类物质与根节点物质同类 因为一共就三类，所以用这类取余的做法还是很妙的

核心要点

int find(int x){
    if(p[x]!=x){
    int tmp=find(p[x]);
    d[x]+=d[p[x]];
    p[x]=tmp;
    }return p[x];
}

为什么先用tmp存储祖先值? d[x]明明表示到父节点距离，为什么d[x]+=d[p[x]]可以做到d[x]获得到根节点的距离？

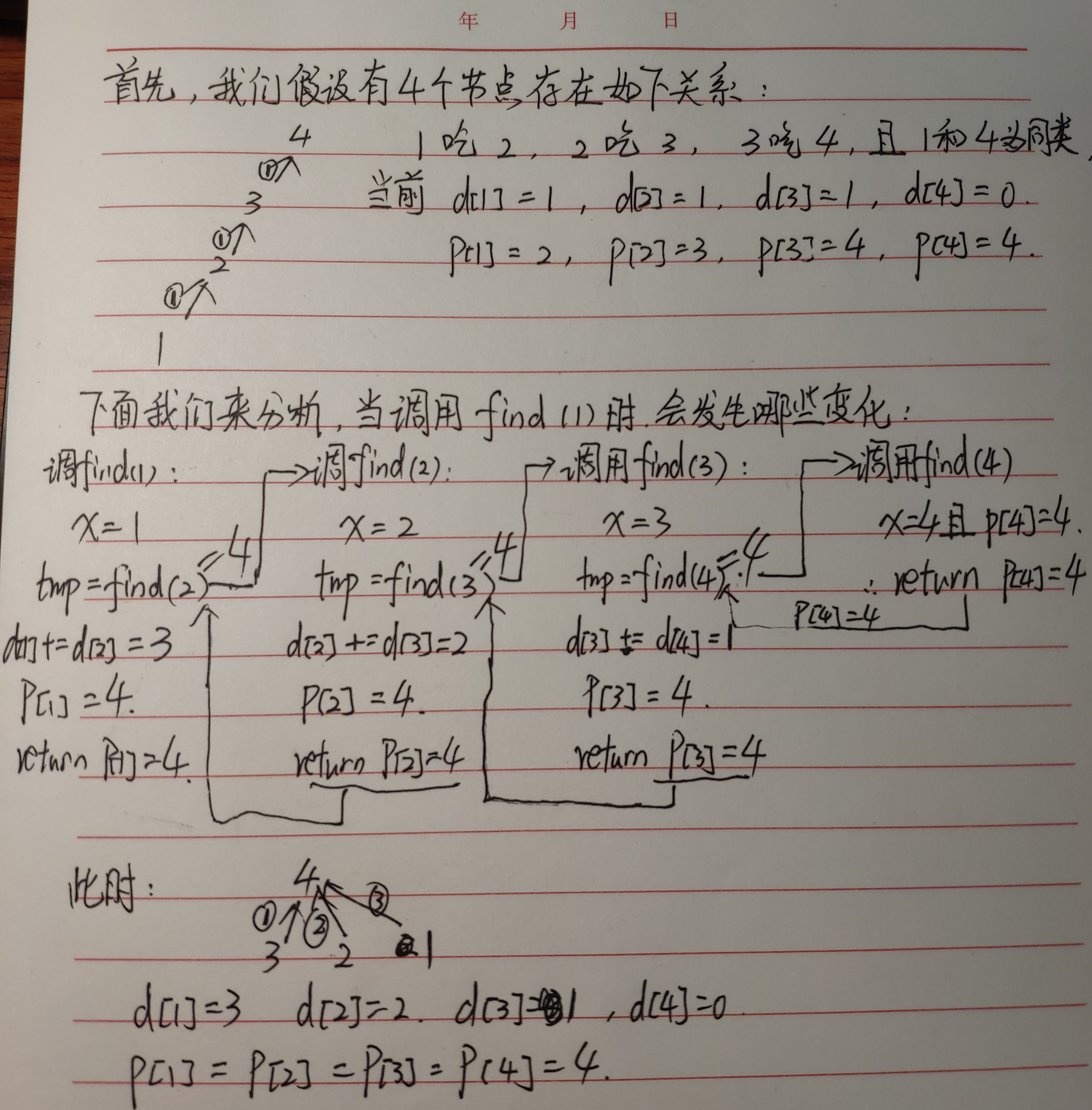
这里我的解释可能不如一张图来的清楚递归状态处理.jpg

另外，对于合并后，距离的处理也很重要食物链网课截图.png

以图为例，图中的 X 与 Y 为同类，那么 X 的祖先 PX 可以修改其祖先为 Y 的祖先 PY 这样合并后，PX 到 PY 的距离怎么处理？

因为两者为同类，可以列出图中右边等式(d[x] + d[px]) % 3 = d[y] %3

因此可以将d[y] - d[x]的值直接赋给d[px] 以此实现两者同类

（异类如A吃B，转换方式类似，不再赘述）

感谢各位的阅读，希望能给你带来帮助，欢迎留言

~~hhh，偷题有种犯醉的感觉~~