LeetCode 刷题笔记---（一）

LeetCode刷题笔记---（一）

这里的都是LeetCode提供的字节强关联算法题

ID：2696

给你一个仅由大写英文字符组成的字符串 s 。

你可以对此字符串执行一些操作，在每一步操作中，你可以从 s 中删除 任一个 "AB" 或 "CD" 子字符串。

通过执行操作，删除所有 "AB" 和 "CD" 子串，返回可获得的最终字符串的最小可能长度。

注意，删除子串后，重新连接出的字符串可能会产生新的 "AB" 或 "CD" 子串。

思路历程：

由于太久没刷算法题，导致没有什么概念，一开始只是蛮力地去求解匹配

然后发现可以把检查规则的部分拿出来，作为单独的函数进行递归调用

后来发现，我的递归调用只能满足从中间开始依次向外检查，不能保证类似 AABCDB这类的，因为检测不了两端的AB

开始查看题解，用到了栈，确实，一下就想通了

就类似于消消乐一样，放进去，消除后能继续消除

记录一下CPP 中的vector，定义 vector a ; 方法: push_back(s), pop_back(), size()

STL真厉害...

记住，看完题解后自己重新敲一遍代码，期间不要去看题解了

第一次运行的时候出问题了，debug后发现忘了修改下标，越界访问了

answer：

class Solution {
public:
    int minLength(string s) {
        vector <char> stack;
        int m =0;
        for(char c :s){
            stack.push_back(c);
            m++;
            if(m>=2){
                if(stack[m-2]=='A'&&stack[m-1]=='B'||stack[m-2]=='C'&&stack[m-1]=='D'){
                    stack.pop_back();
                    stack.pop_back();
                    m-=2;
                }
                
            }
        }
        return stack.size();
    }
};

ID:455

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

思路历程：一开始确实考虑到了要排序，但是一看示例已经排好了，而且不确定是否带algorithm库，所以没有用sort，原理还是很简单的，就是贪心

简单的描述就是，排好序后，如果当前饼干数能满足大胃口的小孩，就一定能满足小胃口小孩，所以饼干数一点点变多，然后给刚好能满足的小孩就行

answer：

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        int i=0;
        int j=0;
        int n1=s.size();
        int n2=g.size();
        sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        while(j<n1&&i<n2){
            if(s[j]>=g[i]){
                i++;
            }
            j++;
        }
        return i;
    }
};

感觉其他更快的解没啥算法上的区别，只是一些定义或者底层指针的使用有区别

ID：344

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须**原地修改输入数组**、使用 O(1) 的额外空间解决这一问题。

思路历程：好简单，但是一开始想多了，一开始打算用vector的erase和insert方法实现

但是这只是队列转了一圈

老老实实的手动swap一下就结束了

class Solution {
public:
    void reverseString(vector<char>& s) {
        int length = s.size();
        for (int i=0;i<length/2;i++){
            char t = s[i];
            s[i]=s[length-1-i];
            s[length-1-i]=t;
        }
    }
};

ID：199

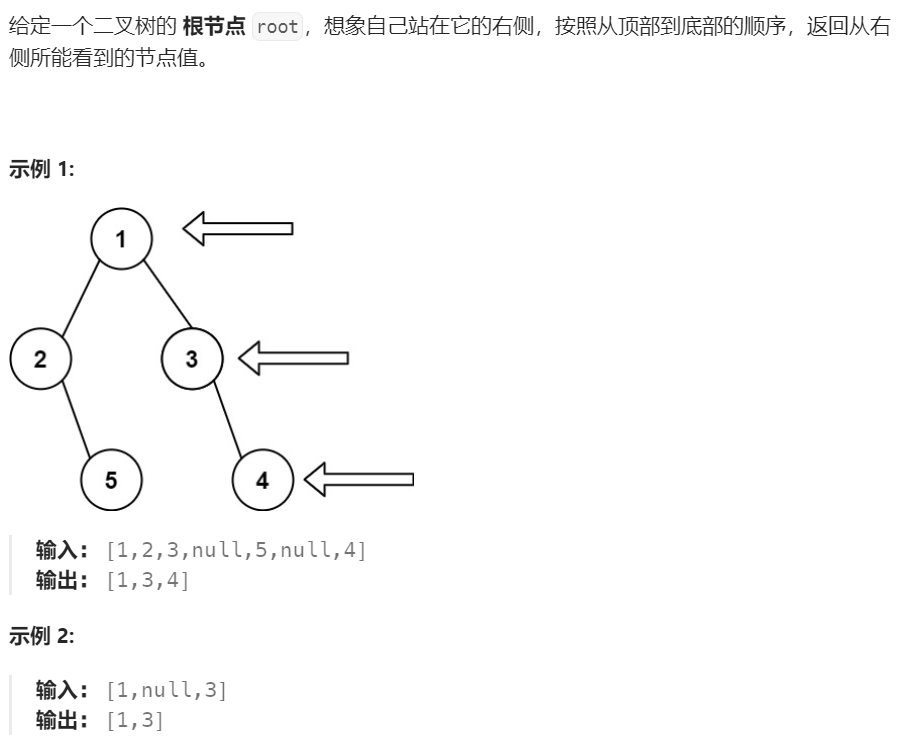
看到题干的时候，已经考虑到，会出现左子树更深的情况了，但是一开始只是想先回顾一下右子树的深度遍历，结果样例就过完了

后来再考虑怎么补救，一开始想的是遍历完右子树后，记住深度，然后检查树的总深度是否一致，但是这样是目光比较短浅的，因为出现新的深度还要再比较。不如直接从整体触发。

看完题解的两个思路总结一下：

深度优先遍历

我们先获取树的总深度，这意味着我们知道了答案的个数

然后深度遍历过程中，访问完根节点后，先访问右子树，再访问左子树即可

每次访问时，要查看深度是否到达右侧最大深度，然后判断是否插入
广度的话优先遍历

就是层序遍历，每层遍历一遍，取出最右侧的节点即可

需要注意的是，数据结构方面：广度一般使用的是队列，而深度一般采用的是栈

看完题解后，使用广度优先回答时，依旧出现了bug，这次的原因主要是对队列特点的混淆

为了每次都拿出最右的节点，我们传入节点时，顺序应该是先左节点，然后右节点

因为先进先出（FIFO）所以最后剩下的节点是最右端的节点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector <int> result;
        queue <TreeNode*> que;
        
        que.push(root);
        while(!que.empty()){
            int count = que.size();
            while(count--){
                TreeNode* tmp = que.front();que.pop();
                if(tmp){
                    if(tmp->left)que.push(tmp->left);
                    if(tmp->right)que.push(tmp->right);
                    if(count==0&&tmp)result.push_back(tmp->val);
                }
            
            }
        }
        return  result;
    }
};

这里有个小细节得debug只后才知道

while(count--)时，count=0才是最后一个节点，而不是count=1

DFS不太好理解，在此就不写题解了（每次都要考虑到当前最大深度）

ID：169

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

![image-20240110145205132](C:\Users\paul zrx\AppData\Roaming\Typora\typora-user-images\image-20240110145205132.png)

比较简单，我用的是map，虽然磕磕碰碰，但是做出来了（比较慢

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n =nums.size();
        int res;
        map<int,int> all;
        for(int c:nums){
            if(all.find(c)==all.end()){
                all[c]=1;
            }else{
                all[c]++;
            }
        }
        for(auto c:all){
            if(c.second>n/2)res=c.first;
        }
        return res;
    }
};

稍微比较快一点的做法是，直接排序，然后下标直接遍历过去，计数器变化，既然一定有多数元素，那就一定会有计数器符合条件。

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int count = 0;
        sort(nums.begin(),nums.end());
        for(int i = 0;i<nums.size() - 1;i++)
        {
            if(count >= nums.size()/2)return nums[i];
            if(nums[i+1] == nums[i])count++;
            else count = 0;
        }
        return nums.back();
    }
};

ID：3

其实看到题目之后就知道是滑动窗口了，但是真的不知道该怎么做（之前了解过，但是没做过，也没背过模板）

一开始的思路就是暴力：

但是发现，如果是窗口的话，应该要有首尾两个指针比较好，窗口内未重复就移动尾指针，重复了就同时移动首尾指针。这里判断重复的方法如果不用遍历的话，就用哈希表

最后窗口的长度就是无重复子串的长度

这个思路有点麻烦了，可以简化一下

比如我们现在尾指针自动遍历，头指针在尾指针发现重复字符后，自动跳到重复字符的上个位置，这样即可保证窗口内部是没有重复字符的，并记录当下的最大长度即可

这样就避免了遍历检查窗口内是否重复的问题

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        
        map<char, int> dic;
        int lenght=s.size();
        int i= -1;
        int j= 0;
        int res=0;
        while(j<lenght){
            if(dic.find(s[j])!=dic.end()){//重复，更新左指针
                i=max(i,dic[s[j]]);
            }
            //不管有没有重复，都要更新map
            dic[s[j]]=j;
            res=max(res,j-i);
            j++;
        }
        return res;
    }
};

DP属实有点难度，而且题解还做了优化，减少了空间复杂度，只用三元计算保留了比较值

附一张核心图

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> dic;
        int res = 0, tmp = 0, len = s.size(), i;
        for(int j = 0; j < len; j++) {
            if (dic.find(s[j]) == dic.end()) i = - 1;
            else i = dic.find(s[j])->second; // 获取索引 i
            dic[s[j]] = j; // 更新哈希表
            tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
            res = max(res, tmp); // max(dp[j - 1], dp[j])
        }
        return res;
    }
};

ID：146

这题实在是不好说，难也不算特别难，用双向链表做，不管是get还是put的时候都更新一下状态，放到链表尾部，然后容量不够了把链表头部（最不常用）的去掉

有一说一，真的很难完全写出来

自己写的话，要对链表的一系列引用非常熟悉，我写一半感觉没啥作用，就停下来了，等下次复盘吧，这次先把几个大类过一遍