P4ul
文章
45
分类
14
评论
8

LeetCode 刷题笔记---（四）

| 算法 •
字数总计 8057 | 阅读时长 20分钟 | 阅读量 37

LeetCode刷题笔记---（四）

今天应该能把字节刷完，然后再刷一两道就去完成别的任务

ID：31

image-20240113141431528

讲道理，如果nums长度不大的话，可以直接拿出所有数，然后作为一个十进制数，全排列出所有结果，然后取出后一个结果的排列就行

但是nums.length可以到100，这样显然不太行了

尝试了一下，不太会

看完题解后，自己写了一遍，会了，但依旧磕磕绊绊，复盘一下

其实我写的也是对的，只不过，找到升序之后我直接进行了交换，忘记从尾部开始重新找值交换

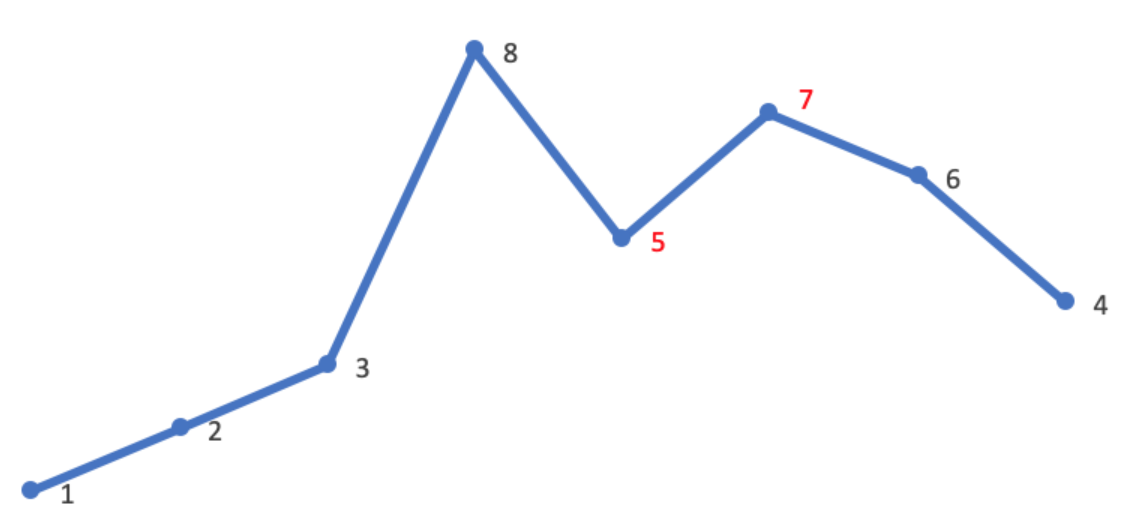
image-20240113144248668

  • 从后往前找到升序序列，没找到就sort一下返回答案

  • 找到后，从后往前找打第一个大于升序前节点的值，进行交换

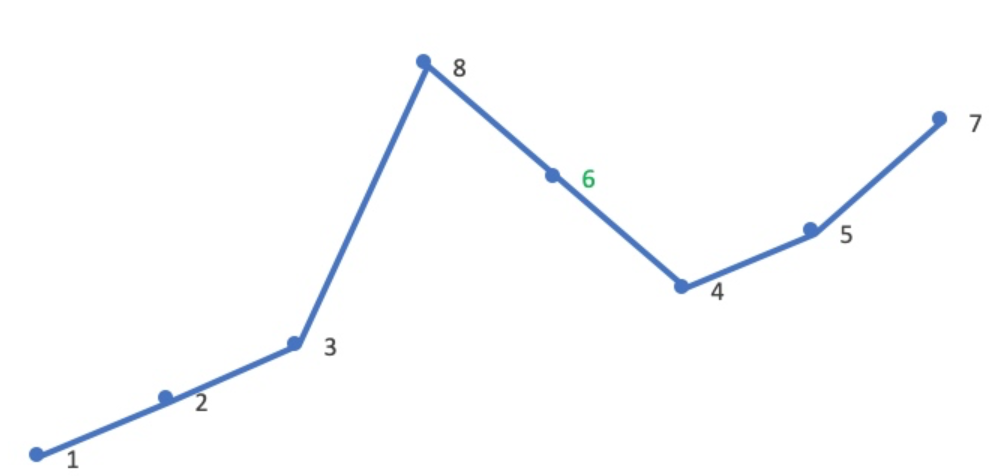
image-20240113144540492

  • 现在升序后节点开始都是降序了，需要重新排列一下，我就直接双指针swap了

answer：

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int n = nums.size();
        if(n==1)return;
        int j=n;
        while(j--){
            if(j>0&&nums[j]>nums[j-1]){
                break;
            }
        }
        if(j<0){
            sort(nums.begin(),nums.end());
        }else{
            int i=n;
            while(i--&&i>j){
                if(nums[i]>nums[j-1])break;
            }
            swap(nums[i],nums[j-1]);
            n--;
            while(n>0&&n>j){
                swap(nums[n],nums[j]);
                n--;j++;
            }
        }
        
    }
};

这道题给我的提示是，下次可以先画图，再充分思考，每次直接思考很可能只能做对部分情况

ID：310

题目有点长，我直接示例了

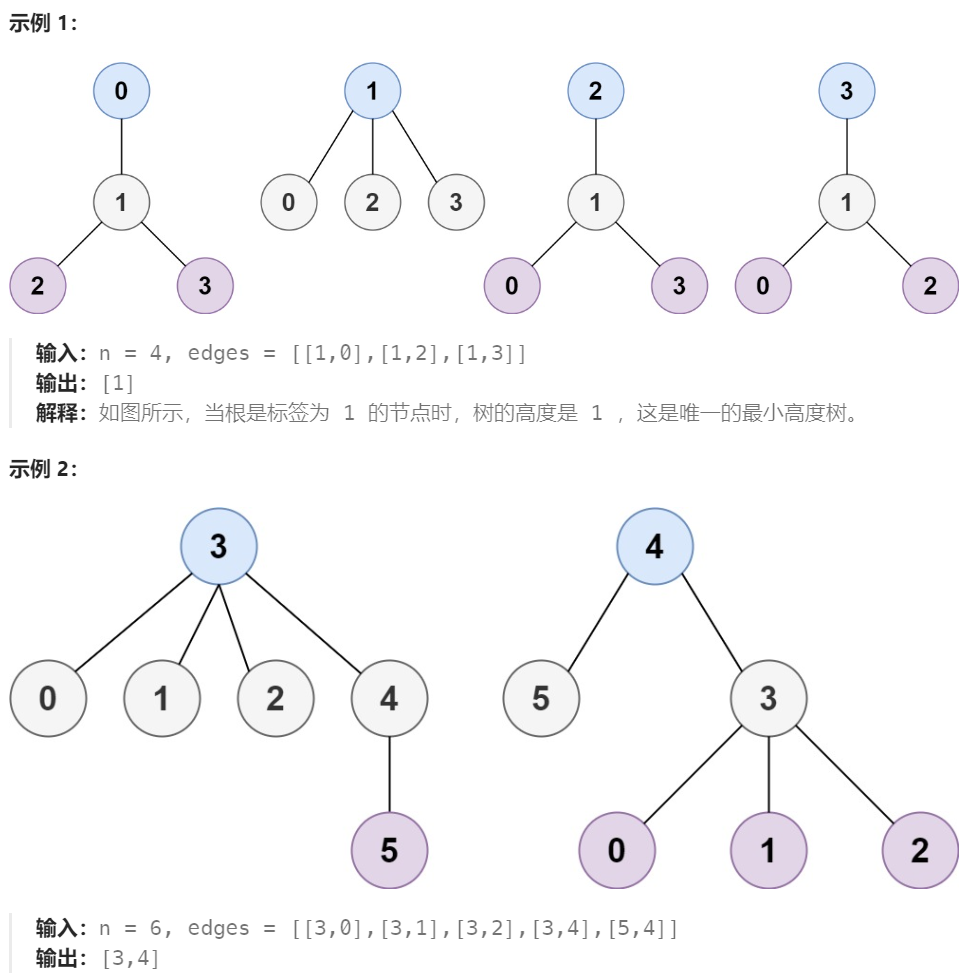
image-20240113145320976

思路历程：把所有点都拿出来，然后放入map，然后BFS，记录深度，如果深度变小，就清空之前的结果，将当前根节点存入，如果深度一致，就追加

细节：map里面放无向路径

唉，还是超时了，暴力求解感觉有点慢，感觉在其中如果提早加判断会好一点（没啥用

超时答案

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        map<int,vector<int>> hash;
        vector<int> res;
        queue<int> que;
        int mindp=20000;
        if(n==1)return {0};
        for(auto c : edges){
            hash[c[0]].push_back(c[1]);
            hash[c[1]].push_back(c[0]);
        }
        for(auto c:hash){
            que.push(c.first);
            int depth=0;
            map<int,int> visit;
            while(!que.empty()){
                int count=que.size();
                    while(count--){
                        int tmp=que.front();que.pop();
                        visit[tmp]=1;
                    for(int node:hash[tmp]){
                        if(visit.find(node)==visit.end())que.push(node);
                    }
                }
                depth++;
                
            }
            if(mindp>=depth){
                if(mindp>depth)res={};
                res.push_back(c.first);
                mindp=depth;
            }
        }
        return res;
    }
};

看题解吧

一开始真的看不懂，后来换了个思路理解了一下，醍醐灌顶

如果所有节点都在一条线上，那么我拎起线上一点，线会折起来，我希望折起来后的长度最短，是不是拎起中点最好。

哪怕有其他线搭在这根线上，只要我能保证这条线是最长的，就能符合要求

那么问题是怎么找到这无向无环图里最长的路径呢？

任意点出发，找到最远点a，从a出发找到最远点b，ab即最长路径。

算法导论提供了证明

举个特殊例子方便大家理解的话，可以看作是椭圆边上的节点出发，如何找到椭圆上的最长弦。

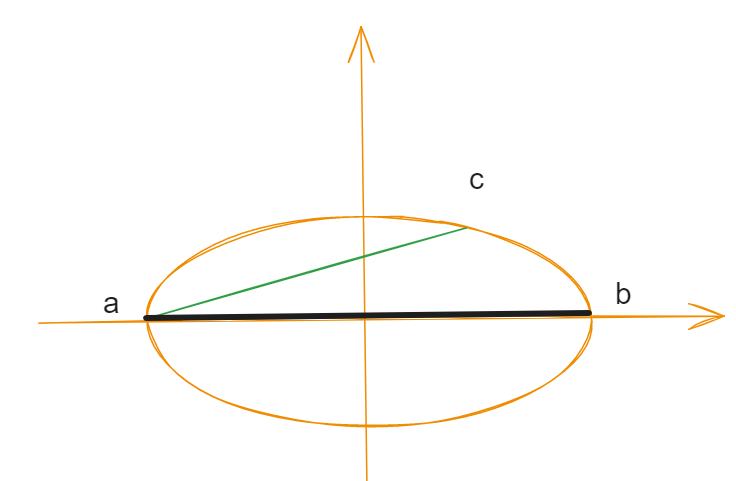
image-20240113180720120

点c会先找到点a，然后点a会找到点b，ab即为最长路径（这个只可意会，因为细想是有bug的）

但是这样其实比较麻烦，因为无向图你去找最远路径比较难，要记录父亲节点才能逆向推回来

我们可以再思考一下，拎起来的点可以是中点（奇数个）可以是两个点（偶数），然后从边缘剪枝（度为1）

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        map<int, vector<int>> hash;
        vector<int> res;
        queue<int> que;
        vector<int> du(n, 0);
        int mindp = 20000;
        if (n == 1)
            return {0};
        for (auto c : edges) {
            hash[c[0]].push_back(c[1]);
            hash[c[1]].push_back(c[0]);
            du[c[0]]++;
            du[c[1]]++;
        }
        for (int i = 0; i < n; i++) {
            if (du[i] == 1)
                que.push(i);
        }
        int rest = n;
        while (rest > 2) {
            int count = que.size();
            while (count--) {
                int tmp = que.front();
                que.pop();
                rest--;
                du[tmp] = 0;
                for (int c : hash[tmp]) {
                    du[c]--;
                    if (du[c] == 1)
                        que.push(c);
                }
            }
        }
        while (!que.empty()) {
            res.push_back(que.front());
            que.pop();
        }
        return res;
    }
};

泪目了，终于过了

重新写那道LRU内存

c++在定义结构体时，记得提前写好构造函数，例如

struct DLinkedNode {
    int key, value;
    DLinkedNode* prev;
    DLinkedNode* next;
    //以下为构造函数
    DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
    DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};

对应类也一样，比如

LRUCache(int _capacity): capacity(_capacity), size(0) {
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head->next = tail;
        tail->prev = head;
    }

提前写好双向链表的基本操作（插入节点至开头）（删除节点）--> 移动节点

struct DLinkedNode {
    int key, value;
    DLinkedNode* prev;
    DLinkedNode* next;
    DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
    DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};

class LRUCache {
private:
    unordered_map<int, DLinkedNode*> cache;
    DLinkedNode* head;
    DLinkedNode* tail;
    int size;
    int capacity;

public:
    LRUCache(int _capacity): capacity(_capacity), size(0) {
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head->next = tail;
        tail->prev = head;
    }
    
    int get(int key) {
        if (!cache.count(key)) {
            return -1;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        DLinkedNode* node = cache[key];
        moveToHead(node);
        return node->value;
    }
    
    void put(int key, int value) {
        if (!cache.count(key)) {
            // 如果 key 不存在，创建一个新的节点
            DLinkedNode* node = new DLinkedNode(key, value);
            // 添加进哈希表
            cache[key] = node;
            // 添加至双向链表的头部
            addToHead(node);
            ++size;
            if (size > capacity) {
                // 如果超出容量，删除双向链表的尾部节点
                DLinkedNode* removed = removeTail();
                // 删除哈希表中对应的项
                cache.erase(removed->key);
                // 防止内存泄漏
                delete removed;
                --size;
            }
        }
        else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            DLinkedNode* node = cache[key];
            node->value = value;
            moveToHead(node);
        }
    }

    void addToHead(DLinkedNode* node) {
        node->prev = head;
        node->next = head->next;
        head->next->prev = node;
        head->next = node;
    }
    
    void removeNode(DLinkedNode* node) {
        node->prev->next = node->next;
        node->next->prev = node->prev;
    }

    void moveToHead(DLinkedNode* node) {
        removeNode(node);
        addToHead(node);
    }

    DLinkedNode* removeTail() {
        DLinkedNode* node = tail->prev;
        removeNode(node);
        return node;
    }
};

今天3题写了好久

尤其是中间那道，一开始真想不明白...

力扣字节专题完结撒花！

继续加油吧

文章作者： P4ul
本文链接：
版权声明： 本站所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 打工人驿站！
算法 c++
喜欢就支持一下吧
打赏
微信 微信
支付宝 支付宝