P4ul
文章
44
分类
14
评论
6

LeetCode 刷题笔记---（五）

| 算法 •
字数总计 9051 | 阅读时长 22分钟 | 阅读量 27

LeetCode 刷题笔记---（五）

今天刷hot100

ID：35

二分查找，找不到就按顺序插入

简单的练练手

answer：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int i=0;
        int j=nums.size();
        int res=0;
        while(i<j){
            int mid=(i+j)/2;
            if(mid==i)break;
            int privot=nums[mid];
            if(target>privot){
                i=mid;
            }else if(target<privot){
                j=mid;
            }else return mid;
        }
        if(target>nums[i])return j;
        else return i;
    }
};

ID：34

上一题的进阶版，二分查找，要求返回target的最早下标，最迟下标

思路历程：

一开始想的是，二分查找，然后找到后，将结果存入vector res，结果没考虑到找到后下标怎么变化。

后来想通了，简单一点，找到后就break；

出循环后分两种情况：

  • 如果l==mid，说明是循环条件不满足退出的

    判断nums[i]==target，因为j是一定会被遍历到的，i不一定，所以要判断，如果符合，就返回两个i

    如果不符合说明没找到，返回{-1,-1}

  • 如果i !=mid，说明是找到了退出的，那么左右指针初始化为mid，然后分别往左往右，返回左右指针

answer：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int i=0;
        int j=nums.size();
        int mid;
        if(nums.empty())return {-1,-1};
        while(i<=j){
            mid=(i+j)/2;
            if(mid==i)break;
            int privot =nums[mid];
            if(target>privot){
                i=mid;
            }else if(target<privot){
                j=mid;
            }else{
                break;
            }
        }
        int l=-1,r=-1;
        if(i==mid){
            if(nums[i]==target){
                return{i,i};
            }else{
                return{-1,-1};
            }
        }
        l=r=mid;
        while(l>=0&&nums[l]==target)l--;
        while(r<nums.size()&&nums[r]==target)r++;
        return{l+1,r-1};
    }
};

ID：64

image-20240120150942226

和之前的路径选优差不多，也是DP的思想

思路历程：

先遍历第一行第一列，初始化第一行、第一列的结果

然后判断是否为单行单列，是的话可以直接返回结果

如果不是，就一层层遍历下去，当前格子的最优解=min(左边的最优解，上面的最优解)+当前格子的值

answer：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        vector<vector<int>> map;
        map=grid;
        int i=1,j=1;
        while(i<m){
            map[i][0]=map[i-1][0]+grid[i][0];
            i++;
        }
        while(j<n){
            map[0][j]=map[0][j-1]+grid[0][j];
            j++;
        }
        if(m==1)return map[0][n-1];
        if(n==1)return map[m-1][0];
        i=j=1;
        while(i<m){
            j=1;
            while(j<n){
                map[i][j]=min(map[i-1][j],map[i][j-1])+grid[i][j];
                j++;
            }
            i++;
        }
        return map[m-1][n-1];
    }
};

BFS会更好吗？其实不一定，斜着一层层遍历，不一定会比行列的遍历更快

ID：230

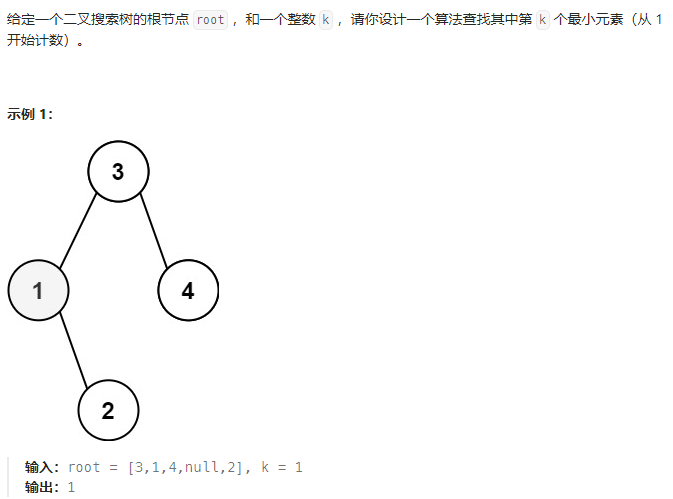
image-20240120154818977

思路历程：

一开始没看到是二叉搜索树，看到左孩子<父亲节点<右孩子 才记起来

然后再想DFS，很惭愧。。。一开始一直想用栈

后来发现用函数递归巨快无比。。。

answer：

class Solution {
public:
void dfs(TreeNode*tmp){
    if(tmp->left)dfs(tmp->left); 
    res.push_back(tmp->val);
    if(tmp->right)dfs(tmp->right);
}
vector<int> res;
    int kthSmallest(TreeNode* root, int k) {
        dfs(root);
        return res[k-1];
    }
};

ID：238

image-20240120160235291

思路历程：

。。。不要使用除法。。。

不太会，看题解了

看到了前缀积和后缀积，有了点想法

就是在第一次遍历的时候，开个数组记录前n个积，开个数组记录后n个积

然后第二次遍历就可以实现前缀积与后缀积相乘得到结果

answer：

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n=nums.size();
        if(n==2)return{nums[1],nums[0]};
        vector<int>head(n);
        vector<int>tail(n);
        vector<int>res(n);
        int i=1,j=n-1;
        head[0]=nums[0];tail[n-1]=nums[n-1];
        while(i<n-1){
            head[i]=head[i-1]*nums[i];
            tail[j-i]=tail[j-i+1]*nums[j-i];
            i++;
        }
        i=1;
        res[0]=tail[1];res[n-1]=head[n-2];
        while(i<n-1){
            res[i]=head[i-1]*tail[i+1];
            i++;
        }
        return res;
    }
};

有一说一，第一次遇到前缀的概念，挺新颖的，让我想起了字节一面的那道题目

其实只要每行数组取出最大前缀和，然后记录下标，每次继续下去要成为负数就去其他路加回正的，

如果加不回来，就换条路先走

每条路到达最大值后就停下来，这条路的使命就完成了

ID：72

image-20240120162740333

思路历程：

一开始想着先判断字符长度，如果相等，就判断相同下标是否一致，然后总数-一致数（不对的）

然后不相等的情况下，拿短的字符串在长字符串中寻找，如果顺序一致可以减去一致数

但是这个找到顺序一致有点难啊，

主要是find没搞清楚返回了什么，没找到的话会返回一个很大的数

然后字符串不同的通过了一些，相同的又不会了

看了题解，居然是DP问题。。。

（有点难，需要缓一缓）

ID：234

简单的回文判断（链表）

我觉得下次可以直接用简单的想法，没必要想很多奇奇怪怪的数据结构

看题解的时候可以欣赏，但是做题的时候要先保证能做出来

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector<int> all;
        ListNode* tmp=head;
        if(!head->next)return true;
        int count=0;
        while(tmp){
            count++;
            all.push_back(tmp->val);
            tmp=tmp->next;
        }
        int i=0;
        while(i<=count/2){
            if(all[i]!=all[count-i-1])return false;
            i++;
        }
        return true;
    }
};

有的用递归做的，可以减少空间。。。有点看不懂代码，虽然能理解一点

还有一种快慢指针的，快指针是慢指针的两倍速，然后到结尾了，慢指针刚好到中间

然后中间开始反转链表，然后快指针从尾部，头指针从头部遍历并判断

ID：84

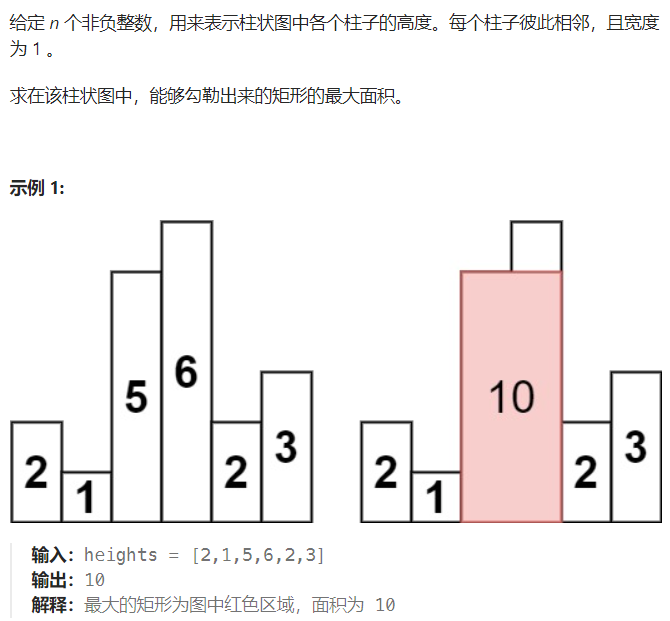
image-20240120235601805

思路历程：

很难的一道DP题，虽然知道很多时候该怎么选择，但是有些样例就是考虑不到，关于下一块到来时，我要考虑的有：

  • 要不要加上这一块（过去的大小和接收这块后的大小）

    这里的接受这块后的大小，是由最小块决定的？是但是范围不一样，最小块也不一样

    i是遍历的右指针，head是左指针，一般来说只有重新开始的情况要变化

    但是会有问题，就是没有重新开始，但左指针移动会使结果变大

    如12345，我的左指针从2开始到4

    2*3>4 && 2*3>2*2，所以左指针没动，所以问题在于，如果这块是5，他也不会动，至少我的方案是这样，但其实应该动了，因为2*3=3*2，应该左指针后移了因为这样可以提高短板

  • 要不要重新开始（这块太大了，比我之前的res都大太多了）

看题解吧

。。。居然不是DP，第一次见到单调栈

真的花了我好长时间，我是第二天起来才写好的

使用单调栈的过程中记得注意，入栈的时候一定要递增而不是非递减，

出栈的时候遇到小于自己的才停下（不能相等）

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n=heights.size();
        int i=1;
        int res=heights[0];
        vector<int> left(n);
        vector<int> right(n);
        if(n==1)return heights[0];
        if(n==2)return max(max(heights[0],heights[1]),min(heights[0],heights[1])*2);
        int head=0;
        stack<pair<int,int>> stk;
        stk.push({heights[0],0});
        left[0]=-1;
        right[n-1]=n;
        int nowleft=-1;
        while(i<n){
            auto now=stk.top();
            if(now.first<heights[i]){
                stk.push({heights[i],i});
                left[i]=now.second;
            }else{
                while(!stk.empty()){
                    if(stk.top().first>=heights[i]){
                        stk.pop();
                    }else break;
                }
                if(!stk.empty()){
                    left[i]=stk.top().second;
                }else{
                    left[i]=-1;
                }
                stk.push({heights[i],i});
            }
            i++;
        }
        while(!stk.empty())stk.pop();
        i--;
        stk.push({heights[i],i});
        while(i--){
            auto now=stk.top();
            if(now.first<heights[i]){
                stk.push({heights[i],i});
                right[i]=now.second;
            }else{
                while(!stk.empty()){
                    if(stk.top().first>=heights[i]){
                        stk.pop();
                    }else break;
                }
                if(!stk.empty()){
                    right[i]=stk.top().second;
                }else{
                    right[i]=n;
                }
                stk.push({heights[i],i});
            }
        }
        for(i=0;i<n;i++){
            int m=(right[i]-left[i]-1)*heights[i];
            res=max(res,m);
        }
        return res;
    }
};

ID：72 我下次再补吧

文章作者： P4ul
本文链接：
版权声明： 本站所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 打工人驿站！
算法 c++
喜欢就支持一下吧
打赏
微信 微信
支付宝 支付宝