LeetCode 刷题笔记---（六）

看理论看累了，过来刷会儿

ID:283

思路历程：

看上去很简单，但其实还是要一点时间的，我觉得每次做题的时候真的不能犹豫，该用STL就用，别怕，大不了做出来了等面试官提额外要求，犹豫会浪费很多时间

解题思路：记录含0下标，vector进行erase()，注意这里的erase最好从最后开始，不然数组下标会变

answer：

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int n =nums.size();
        if(n==1)return;
        int i=0;
        vector<int>xb;
        while(i<n){
            if(nums[i]==0){
                xb.push_back(i);
            }
            i++;
        }
        int c=xb.size();
        while(c--){
            nums.erase(nums.begin()+xb[c]);
            nums.push_back(0);
        }
    }
};

题解思路：右指针从开头向后遍历，遇到非零的就放在开头（与开头的左指针替换）左指针右移

左指针的左边就是已经完成的序列

ID：20

居然又刷到了简单题

虽然简单，用栈就能解决，但也花了一点时间

主要是逻辑运算没搞好

注意||两边要带括号

answer：

class Solution {
public:
    bool isValid(string s) {
        stack<char> stk;
        int i = 1;
        int n = s.size();
        if (n == 1)
            return false;

        stk.push(s[0]);
        while (i < n) {
            if (!stk.empty()) {
                char tmp = stk.top();
                if (tmp == '(' && s[i] == ')'){
                    stk.pop();i++;continue;
                }
                if (tmp == '[' && s[i] == ']'){
                    stk.pop();i++;continue;
                }
                if (tmp == '{' && s[i] == '}'){
                    stk.pop();i++;continue;
                }
                stk.push(s[i]);
            } else {
                stk.push(s[i]);
            }
            i++;
        }
        if (stk.empty()) {
            return true;
        } else{
            return false;
        }
    }
};

题解里有一个很牛的思路

class Solution {
    public boolean isValid(String s) {
        int length = s.length() / 2;
		for (int i = 0; i < length; i++) {
			s = s.replace("()", "").replace("{}", "").replace("[]", "");
		}
		return s.length() == 0;
    }
}

很厉害，一开始想有点难想到

ID：23

虽然30minAC了，但是运行时间好长，近600ms

其他人只要20ms吗。。。

思路历程：

所有的list转成队列，然后取对头最小元素插入链表

answer：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int n=lists.size();
        int nul=0;
        for(auto c:lists){
            if(c==nullptr){
                nul++;
            }
        }
        if(n==nul)return{};
        vector<queue<int>> all;
        ListNode* res=new ListNode();
        ListNode* head=res;
        int count=0;
        for(auto c:lists){
            queue<int> tmp;
            while(c){
                count++;
                tmp.push(c->val);
                c=c->next;
            }
            all.push_back(tmp);
        }
        while(count--){
            int minhead=10000;
            int idx;
            for(int i=0;i<n;i++){
                if(!all[i].empty()&&minhead>all[i].front()){
                    minhead=all[i].front();
                    idx=i;
                }
            }
            ListNode* node=new ListNode();
            if(count==0)node=nullptr;
            res->val=minhead;
            res->next=node;
            res=node;
            all[idx].pop();
        }
        return head;
    }
};

看看他们的优化答案：最小堆（优先队列）

ID：56

唉，一路跟着没过用例改的...

思路历程：

一开始已经想到了，要先排序，但当时想的是，应该要根据平均值排序，但后来发现有的样例过不了，因为有些区间比较大，比如[8,9]和[1,10]这[1,10]肯定要放后面

所以后来改成了根据区间的右边界排，反正左边界可以处理

然后在删除区间的过程中，记得从后往前删

同时记得判断是否要改变左边界（[1,4],[0,10])

answer：

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        int n=intervals.size();
        int i=0;
        sort(intervals.begin(),intervals.end(),[](vector<int>&a,vector<int>&b){
            return a[1]<b[1];
        });
        i=n-1;
        while(i>0){
            if(intervals[i][0]<=intervals[i-1][1]){
                if(intervals[i][0]>intervals[i-1][0]){
                    intervals[i][0]=intervals[i-1][0];
                }
                intervals.erase(intervals.begin()+i-1);
            }
            i--;
        }
        return intervals;
    }
};

ID：32

思路历程：

一开始以为很简单，就是用栈，直到遇到了这个样例

"()(()"

...很尴尬，因为中间的(成了一个隔板，不知道该怎么处理

这个我可以在入栈时判断是否为空，空的话，把结果暂时存起来

但下面这个样例真过不了了...

"(()(((()"

看了题解....居然是dp...

...题解二是栈，我陷入了思维误区，只想着把括号放进去，其实可以把下标放进去，这样每次

可以记录最大状态

核心思路如下：

class Solution {
public:
    int longestValidParentheses(string s) {
        int maxans = 0;
        stack<int> stk;
        stk.push(-1);
        for (int i = 0; i < s.length(); i++) {
            if (s[i] == '(') {
                stk.push(i);
            } else {
                stk.pop();
                if (stk.empty()) {
                    stk.push(i);
                } else {
                    maxans = max(maxans, i - stk.top());
                }
            }
        }
        return maxans;
    }
};

这里的栈底元素-1就是为了计算最深深度

如果出现了我上面说的隔板，就把-1弹出来，把隔板下标放进去

已经放假了，2天没刷题了，寒假好好学，好好刷题，好好准备

ID：141

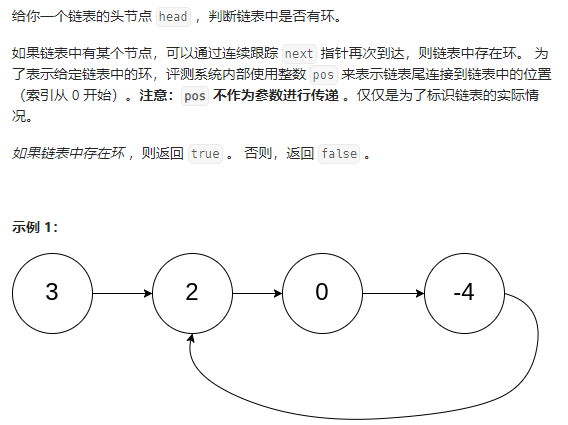
思路历程：

我就是很简单的暴力，用一个map存好节点，如果遇到之前的节点说明有环

answer：

class Solution {
public:
    bool hasCycle(ListNode *head) {
        map<ListNode*, int>node_map;
        ListNode* tmp=head;
        while(tmp){
            if(node_map.find(tmp)!=node_map.end()){
                return true;
            }else{
                node_map[tmp]=1;
            }
            tmp=tmp->next;
        }
        return false;
    }
};

看到一种题解，快慢指针，确实也很不错，快指针遇到null就false

如果有环的话，可以这样理解，一快一慢进入环形跑道，然后快的终将会追上慢的（套圈）

answer:

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(!head||!head->next)return false;
        ListNode* slow=head;
        ListNode* fast=head->next;
        while(slow!=fast){
            if(!fast||!fast->next)return false;
            slow=slow->next;
            fast=fast->next->next;
        }
        return true;
    }
};

ID：11

思路历程：

和之前的那个最大矩形有点像，单调栈和哨兵机制

哈哈哈哈

居然卡着时间线过了，笑死我了，看着示例绕过了一些恶心数据

这次其实也可以用栈的机制，找到最远的稍大值，（没有就比较当前值和加长矩形）

answer：

class Solution {
public:
    int maxArea(vector<int>& height) {
        //找一个最远的比自己大的作为边界
        int n=height.size();
        int i=0;
        int sub_res=0;
        while(i<n){
            if(!height[i]||sub_res/height[i]>(n-i)){
                i++;continue;
            }
            for(int j=i;j<n;j++){
                if(height[j]>height[i]){
                    sub_res=max(sub_res,(j-i)*height[i]);
                }else{
                    sub_res=max(sub_res,(j-i)*height[j]);
                }
            }
            i++;
        }
        return sub_res;
    }
};

看看题解

使用双指针进行操作，两边同时向中间靠拢

ID：98

一道正常的DFS，但是只顾着判断当前子树的正确性，忘记判断整体二叉搜素树的正确性了，在函数封装时，得带上一个最小根值和最大根植才行，这样一层层遍历下去才能判断整体是否正确

另外，在判断值大小的时候，可以同时直接判断有无值，所以只需要一次判断

answer：

class Solution {
public:
    bool helper(TreeNode* root, long long lower, long long upper) {
        if (root == nullptr) {
            return true;
        }
        if (root -> val <= lower || root -> val >= upper) {
            return false;
        }
        return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
    }
    bool isValidBST(TreeNode* root) {
        return helper(root, LONG_MIN, LONG_MAX);
    }
};