LeetCode 刷题笔记（八）

这次的主题是树

hello! 树先生！

ID: 94、104、226

很简单的dfs题

不做解释了

（有一些之前写过，可以通过ID搜索一下相关博客）

ID:101

检验对称二叉树

思路历程：

有一说一，一开始感觉很简单，层序遍历，然后依次比较头尾即可，但后来出现了一些问题

比如头节点怎么办，比如不可以在出序列的同时入序列

后来看了题解，很妙，确实可以直接用递归

像我们只要拿出两个节点即可，比较左节点的左孩子和右节点的右孩子，比较左节点的右孩子和右节点的左孩子

那有人会问，你这只是遍历了一层，下一层怎么办

既然我现在比较的是对称的，那么我将对称节点的左孩子右孩子放入函数，是不是也是对称的？

所以递归可以实现

answer:

class Solution {
public:
    bool dfs(TreeNode* left,TreeNode* right){
        if(!left&&!right)return true;
        if((!left&&right)||(!right&&left))return false;
        return left->val==right->val && dfs(left->right,right->left) &&dfs(right->right,left->left);
    }
    bool isSymmetric(TreeNode* root) {
        return dfs(root,root);
    }
};

ID:543

思路历程：

有一说一，没做过真想不到简便的方法

我只能想到必定是两个叶子节点之间的路径

然后进而想到会不会是dfs左右最深，然后深度相加？

感觉也不太对，因为万一最长路径不经过根节点呢？

看题解了

。。。居然还真是左右dfs最深，深度相加，无非是节点一个个遍历下去以保证不经过根节点的情况也能被排查出来

也可以直接dfs，先获取左右子树深度，然后更新res，这样可以自底向上一层层更新上来

不需要层序遍历了

answer:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res=0;
    int dfs(TreeNode* root){
        if(!root)return 0;
        int left=dfs(root->left);
        int right=dfs(root->right);
        res = max(left+right,res);
        return max(left,right)+1;
    }
    
    int diameterOfBinaryTree(TreeNode* root) {
        dfs(root);
        return res;
    }
};

一开始用的层序遍历，30+ms

优化之后只需要不到10ms

ID:102

非常简单的层序遍历，bfs的思想，不做展开了

ID:108

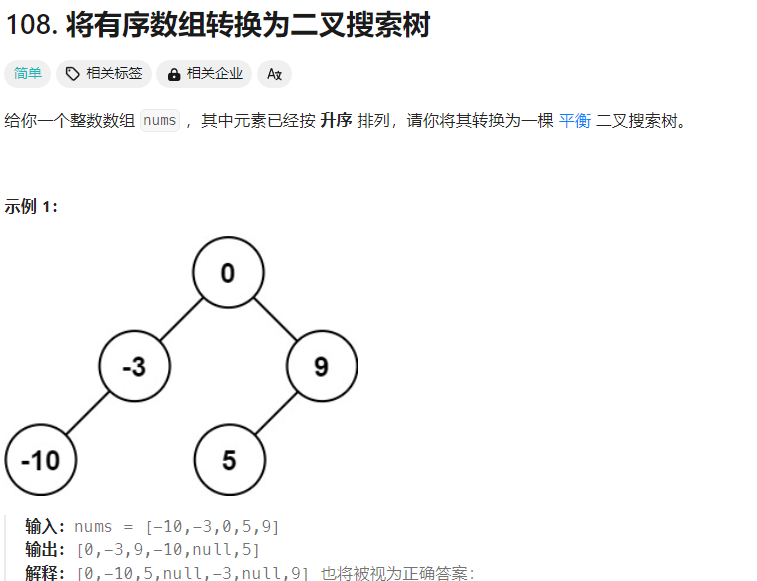
思路历程：

可以想到二分或者说分治，具体让我去实现有点难 (害怕)

...做得少了

看题解了

answer:

class Solution {
public:
    TreeNode* dfs(vector<int>&nums,int left,int right){
        if(left>right) return nullptr;
        int mid = (left+right)/2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left=dfs(nums,left,mid-1);
        root->right=dfs(nums,mid+1,right);
        return root;
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return dfs(nums,0,nums.size()-1);
    }
};

注意传递数组的时候记得使用引用

不然时间差了好几个量级（整个数组拷贝过去了）

ID:98

思路历程：

第二次刷这道题了，又犯了和之前一样的错误，只验证左右孩子是否满足，不考虑整个左右子树

左右子树本身也必须是二叉搜索树

因此在递归时要存储路径上的最大值和最小值状态

还有记得使用long long 类型，因为node.val <= 2^32-1 ，即可以取到int 最大值

answer:

class Solution {
public:
    bool dfs(TreeNode*root,long long lower,long long upper){
        if(!root)return true;
        if(root->val<=lower||root->val>=upper)return false;
        return dfs(root->left,lower,root->val)&&dfs(root->right,root->val,upper);
    }

    bool isValidBST(TreeNode* root) {
        return dfs(root,LONG_MIN,LONG_MAX);
    }
};

ID:199

二叉树右视图，二刷了，很简单的层序遍历，可以看之前的解

ID:114

思路历程:

还是比较简单的，dfs先序遍历存储相应节点，然后再遍历动态数组赋值左右节点即可

(记得赋值左节点，不然会出现环)

answer:

class Solution {
public:
    vector<TreeNode*>res;
    void dfs(TreeNode* root){
        if(!root)return;
        res.push_back(root);
        if(root->left)dfs(root->left);
        if(root->right)dfs(root->right);
    }
    void flatten(TreeNode* root) {
        if(!root)return ;
        dfs(root);
        for(int i=0;i<res.size()-1;i++){
           res[i]->right=res[i+1];
           res[i]->left=nullptr;
        }
    }
};

ID:105

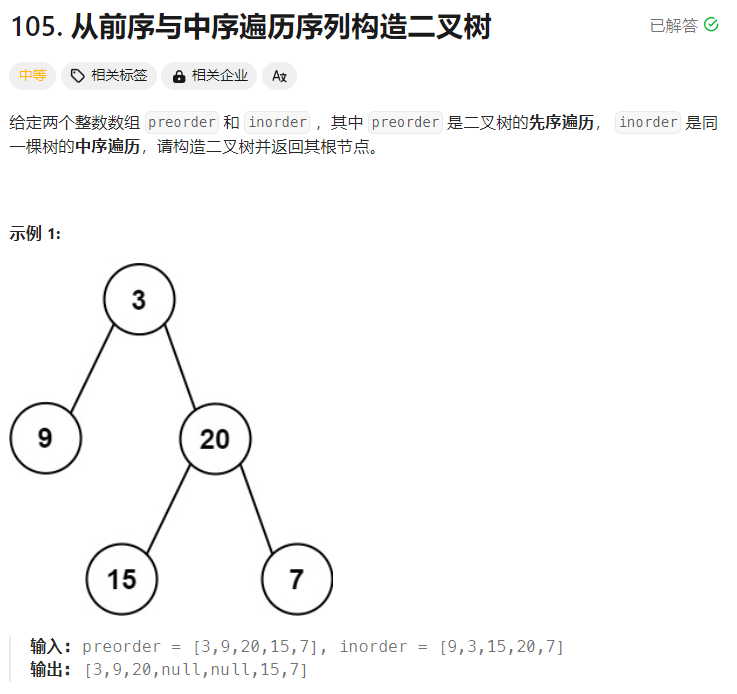
思路历程:

一开始能想到用分治和map，但是具体实现还是不太清楚，因为不知道怎么每次都拿到根节点，先序遍历中万一递归下去不是根节点呢？

这种疑惑是多虑的，每次遍历下去哪怕不是当前根节点，是左孩子，那他也是自己的根节点

我简单概括一下：

就是遍历了先序遍历的数组，以此获取根节点
然后获取中序中根节点的下标，分割左右子树
因为总是左子树先生成，所以先序遍历只要下标递增即可
等左子树都构建结束，才会构建右子树

先序遍历是为了获取根节点，中序遍历是为了确定边界分隔左右子树，同时左右边界可以构造退出递归的条件

answer:

class Solution {
public:
    map<int,int>hash_i;
    int pre_index=0;
    TreeNode* dfs(vector<int>&preorder,vector<int>& inorder,int left,int right){
        if(left>right)return nullptr;
        int mid=hash_i[preorder[pre_index++]];//根节点下标
        TreeNode*root=new TreeNode(inorder[mid]);
        root->left=dfs(preorder,inorder,left,mid-1);//左子树
        root->right=dfs(preorder,inorder,mid+1,right);//右子树
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = inorder.size();
        for(int i=0;i<inorder.size();i++)hash_i[inorder[i]]=i;
        return dfs(preorder,inorder,0,n-1);
    }
};

其实dfs函数内部可以不用inorder数组，因为对应的根节点的值可以直接在 preoerder中获取

ID:437

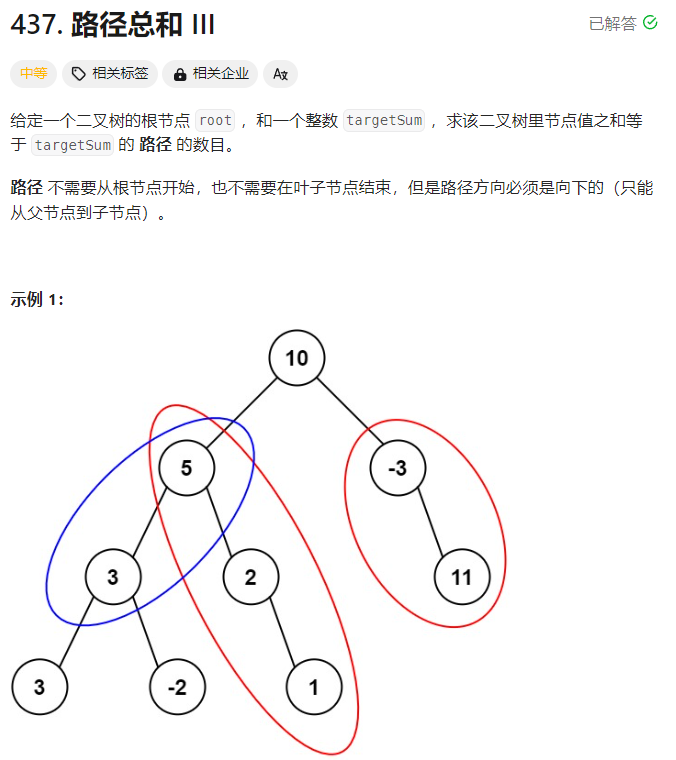
思路历程:

一开始想到dfs都是自底向上，但是不知道怎么自顶向下获取结果

后来想到可以在dfs中target一点点减下去和root->val进行比较

然后为了每个节点都能考虑到，想到了层序遍历

可惜超时了

然后看了题解，发现可以在递归的同时，进行路径的判断

内部的递归负责查找是否有符合条件的路径

外部的递归负责遍历所有节点

tips：最后的类型有overflow的例子，因此要改int为long long

answer:

class Solution {
public:
    int dfs(TreeNode* root,long long targetSum){
        if(!root)return 0;
        int count =0;
        if(root->val==targetSum)count++;
        count +=dfs(root->left,targetSum-root->val);
        count +=dfs(root->right,targetSum-root->val);
        return count;
    }
    int pathSum(TreeNode* root, int targetSum) {
        if(!root)return 0;
        int ans =dfs(root,targetSum);
        ans+=pathSum(root->left,targetSum);
        ans+=pathSum(root->right,targetSum);
        return ans;
    }
};

先短暂总结一下，还有几道难的，下次再联合几道做一下

树的问题一般都利用其特殊的数据结构进行解决

主要的思想还是常用的DFS和BFS

DFS主要是通过递归调用实现；BFS主要是通过queue层序遍历实现

其中可以进行微调，来实现先序、中序、后序遍历等形式

写累了，明天继续加油吧